Controle – Het verkeerslicht
Controlestandaard 530 vereist een steekproefomvang die groot genoeg is om het steekproefrisico (op ten onrechte goedkeuren) aanvaardbaar laag te laten zijn en waarvan de selectie zo is, dat elk element van de te controleren populatie een kans op controle heeft.
Door de steekproef statistisch te onderbouwen is de omvang precies te bepalen uit de vereiste onnauwkeurigheid en de toegestane kans op ten onrechte goedkeuren. Dat professional judgment van pas komt bij het kiezen van deze parameters is vanzelfsprekend. COS 530 laat ook toe dat de wiskundige berekening van de steekproefomvang wordt vervangen door een omvang die gebaseerd is op professional judgment. Ik denk dat dat strijdig is met andere eisen uit diezelfde standaard, zoals het mitigeren van het steekproefrisico.
Controlestandaarden vragen niet alleen om een extrapolatie van de bevindingen maar ook om een expliciete onderbouwing van de hoeveelheid werkzaamheden. Wie niet goedkeurt weet nog niet of dat komt door te veel fouten of door te weinig correcte uitkomsten. Was de populatie bij 0 fouten dan wel goedgekeurd? Zo niet, dan is de steekproef te klein geweest om niet goed te keuren.
Een te grote steekproef kan de verantwoordelijkheid voor de juistheid van de populatie wel eens te veel bij de controleur leggen. Waarom zou de controleur het risico op ten onrechte niet goedkeuren laag houden als de gecontroleerde moet zorgen voor foutloze gegevens? De toelaatbare afwijking is immers geen norm voor hoe veel fouten de populatie mag hebben maar voor de intensiteit waarmee de controleur moet onderzoeken of de populatie aanvaardbaar is.
ISA 530 A3 geeft aan dat de accountant de toelaatbare afwijking bepaalt, wel in twee stappen:
- Een afslag van materialiteit naar uitvoeringsmaterialiteit om het aggregatierisico op te vangen, die verplicht is zodra er sprake is van (des-)aggregatie.
- Een afslag van uitvoeringsmaterialiteit naar toelaatbare afwijking om ruimte te maken voor het vinden van afwijkingen, die niet verplicht is, omdat heel vaak geen afwijkingen worden verwacht.
Het verkeerslichtmodel
Dit model gaat uit van de begrippen maximale en geprojecteerde afwijking. De maximale afwijking staat niet in de COS, maar wel het steekproefrisico op ten onrechte goedkeuren doordat de werkelijke afwijking hoger is dan toegestaan. Het leerboek Statistiek voor Audit en Controlling van Paul Touw en Lucas Hoogduin geeft prima uitleg. De geprojecteerde afwijking is in de COS terug te vinden: de meest waarschijnlijke uitkomst van het bedrag aan afwijkingen in de populatie gegeven de bevindingen in de steekproef. De maximale afwijking is ook een uitkomst van het bedrag aan afwijkingen in de populatie, maar zo hoog dat er maar een kleine kans is (het steekproefrisico) dat dat bedrag nog hoger had moeten zijn.
In dit plaatje staat horizontaal de onbekende afwijking in de populatie en verticaal de kans op een bedrag aan afwijkingen.

(1701-1761)
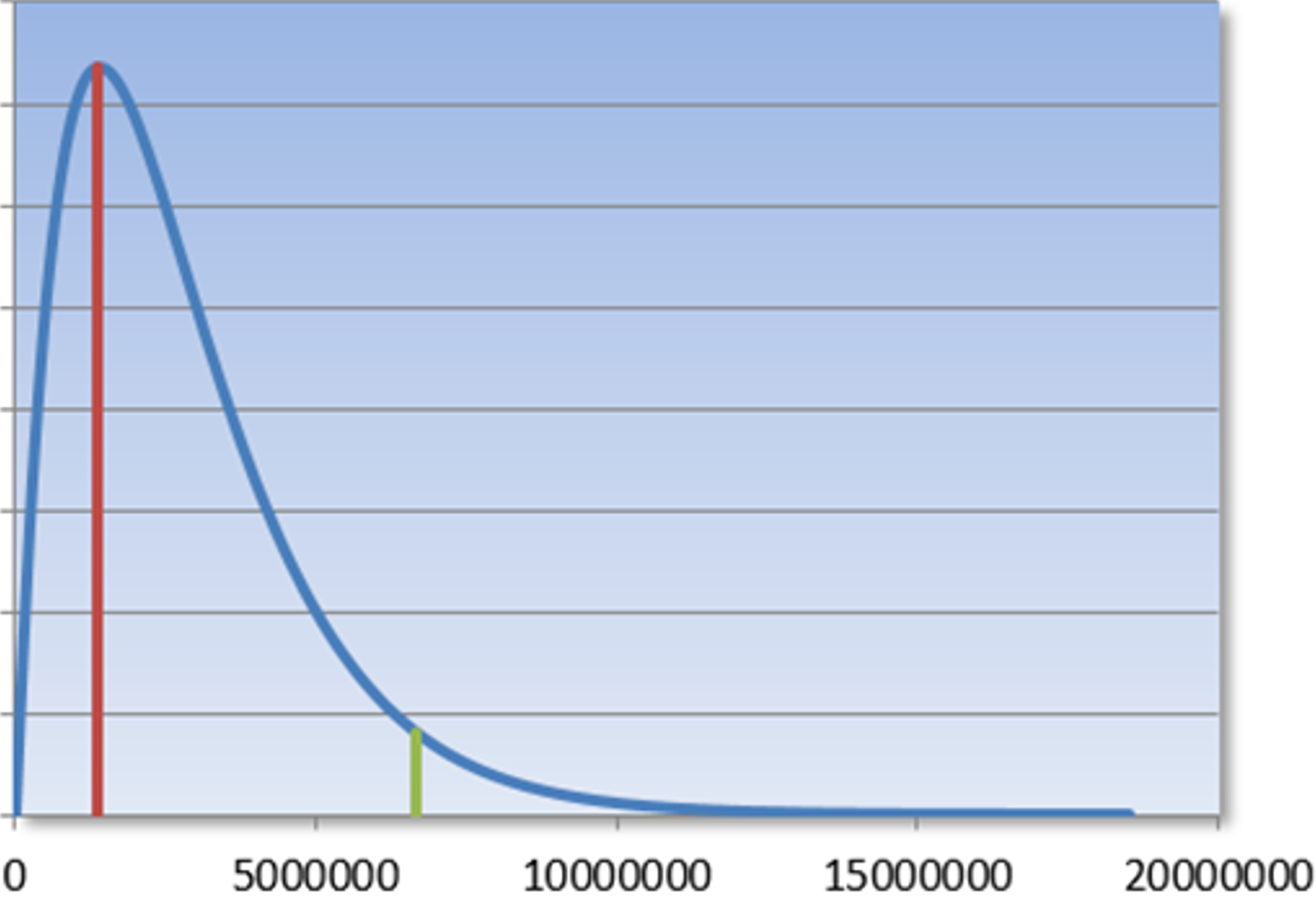
De rode lijn geeft de plek aan van de geprojecteerde afwijking en de groene lijn de maximale afwijking. De oppervlakte rechts van de groene lijn, onder de curve, is het steekproefrisico.
Het model kent drie mogelijke evaluaties van een steekproef:
- Groen – Goedkeuren wanneer de maximale afwijking onder de uitvoeringsmaterialiteit ligt en de geprojecteerde afwijking ter correctie voorleggen om vervolgens het niet gecorrigeerde deel te accumuleren bij de overall evaluatie.
- Oranje – Pas goedkeuren als de gecontroleerde de geprojecteerde afwijking corrigeert, wanneer het verschil tussen maximale en geprojecteerde afwijking onder de uitvoeringsmaterialiteit ligt.
- Rood – Werkzaamheden uitbreiden totdat het verschil tussen maximale en geprojecteerde afwijking onder de uitvoeringsmaterialiteit ligt om de noodzakelijke correctie te kunnen schatten.
Het spreadsheet SMASH24 vergemakkelijkt de berekeningen en ondersteunt bij de discussie hoeveel werk er nu nodig is. Voor de nieuwste versie, zie de pagina Blogs en Downloads. Alle berekeningen komen overeen met de tabellen van Appendix C van de IAASB audit Sampling Guide.
